Как нарисовать
классический лабиринт
Классический лабиринт имеет только одну непрерывную дорогу без разветвлений, поэтому заблудиться в нем невозможно. В английском языке это и есть собственно labyrinth, а более привычный нам лабиринт-путаница (идея которого известна с античности, но первые изображения появляются лишь в XV веке) именуется maze.
На этой странице не объясняется, какие бывают лабиринты, почему именно критский и шартрский типы самые знаменитые и зачем их рисовать. Всем интересующимся темой рекомендуем фундаментальную монографию:
Лабиринты мира [Керн, 2007] – скачать файл формата djvu, 94 Мб
Рисуем лабиринт критского типа
Cretan style labyrinth
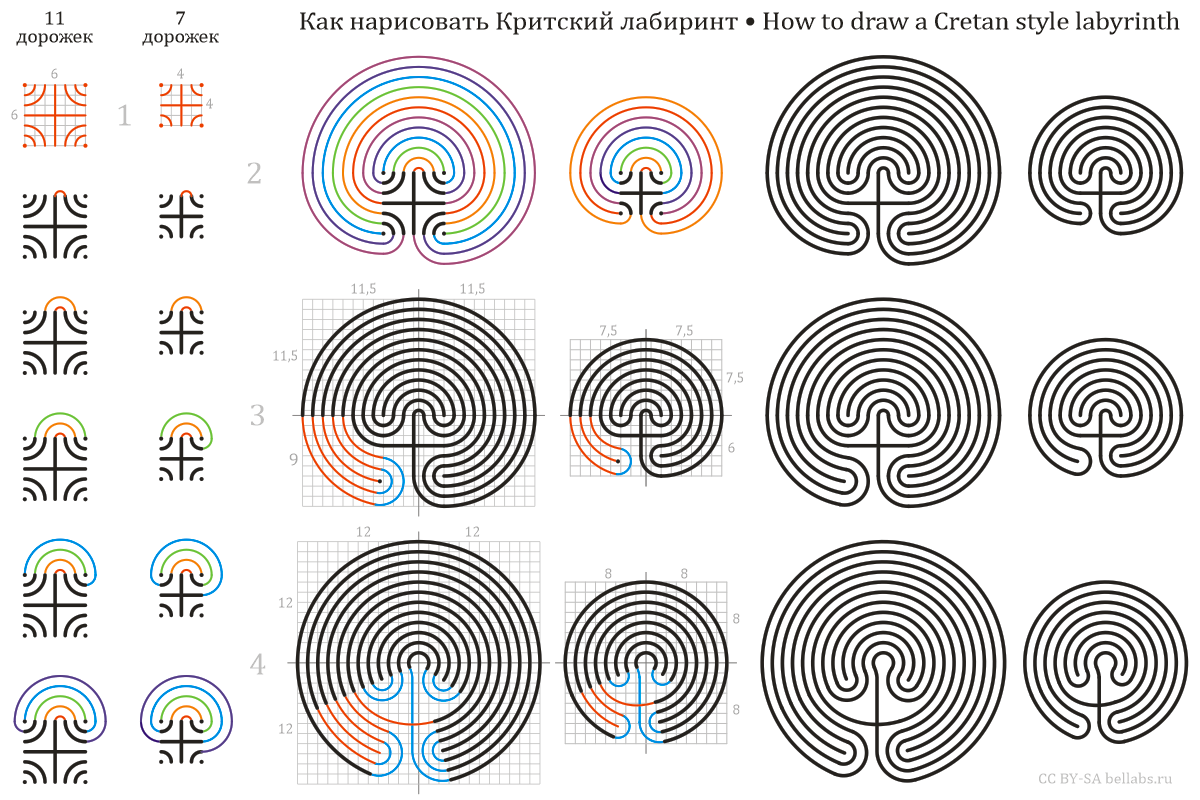
Шаг 1. Исходное построение
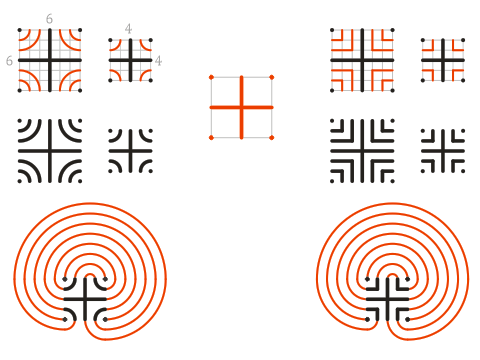
- Быстрый способ построения опирается на несложную крестовидную фигуру:
- Эскизно наметьте произвольный квадрат
- Нарисуйте в центре крест, делящий квадрат на четыре равные части
- По углам квадрата поставьте четыре точки
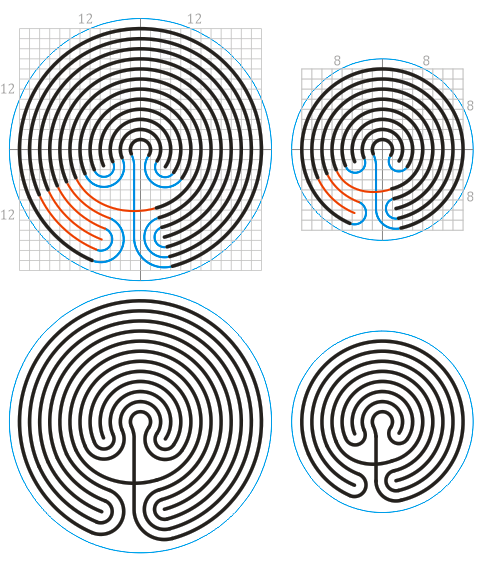
- Критский тип лабиринта может иметь разное количество стенок и дорожек. В зависимости от желаемого размера, нарисуйте нужное число дуг окружностей с центрами в углах квадрата:
- нет дужек – получится лабиринт с тремя дорожками
- по 1 дужке в каждой четверти = 7 дорожек – наиболее распространенный тип (мы его построим)
- по 2 дужки в каждой четверти = 11 дорожек (построим и его тоже)
- по 3 дужки в каждой четверти = 15 дорожек и т.д.
- Вместо «дужек» можно рисовать «уголки» – это никак не влияет на построение лабиринта и на его топологию, изменяется лишь конфигурация внутренних пазух. В дальнейших построениях мы будем использовать «дужки»
Шаг 2. Алгоритм рисования остальных стенок
- Выберите, где будет находиться «центр» лабиринта. Центр – это финальная точка пути по лабиринту, а не середина исходного квадрата. Искомый центр может располагаться в восьми позициях – посередине между четырьмя концами исходного креста и концами ближайших к ним дуг.
- Пусть центр располагается сверху справа. Обведите его полуокружностью, замыкающей верхний конец креста и верхний конец ближайшей дуги справа (маленькая красная полуокружность на схеме).
- Двигаясь от центра лабиринта по сторонам исходного квадрата, найдите ближайший незамкнутый конец слева – и соедините его с ближайшим незамкнутым концом справа (маленькая оранжевая полуокружность над первой красной).
- Продолжайте соединять ближайшие к центру незамкнутые концы слева с ближайшими незамкнутыми концами справа. «Концами» будут служить или точки, или концы исходного креста, или концы исходных дужек.
- В конечном итоге все «концы» исходной фигуры будут соединены стенками – лабиринт готов.
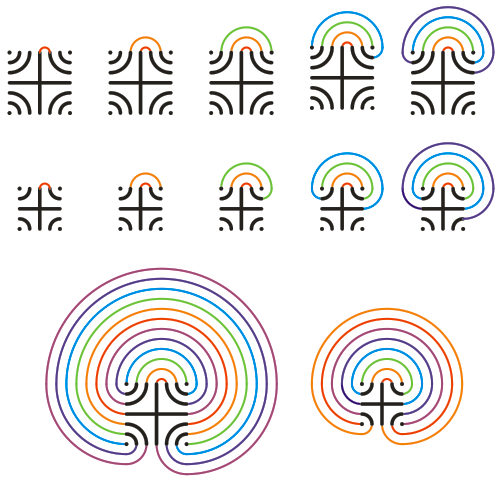
- Легко заметить, что такой лабиринт строится при помощи циркуля: все стенки, кроме исходного креста, состоят из дуг окружностей с центрами в пяти точках – в центре лабиринта и в углах исходного квадрата
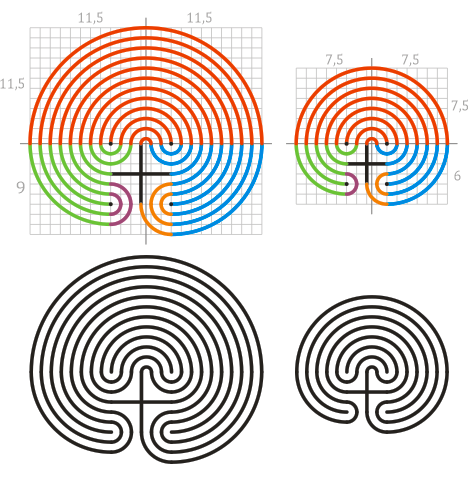
Шаг 3. Симметричность относительно горизонтальной оси
- При геометрически правильном построении лабиринт, однако, получается несимметричным:
- Левая нижняя часть на ширину дорожки выше правой
- Лабиринт асимметричен относительно горизонтальной оси, проходящей через центр: нижняя часть меньше к верхней
- Первый недостаток обычно маскируют небольшим увеличением ширины дорожек в левой нижней части
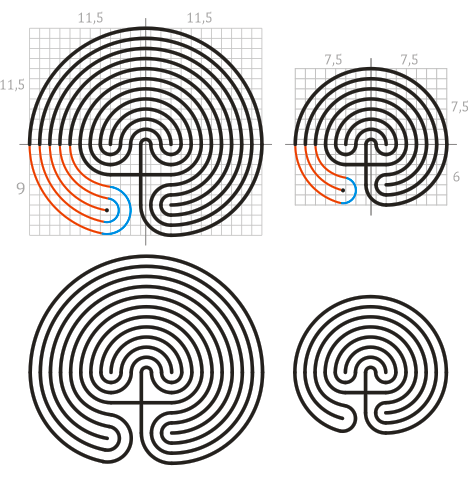
Шаг 4. Симметричность относительно вертикальной оси
- Локальное искажение, предпринятое на предыдущем шаге, не сделает лабиринт «достаточно симметричным», чтобы он смог хорошо вписаться в круг. Простой способ добиться более округлой формы лабиринта на компьютере – растянуть по вертикали нижнюю часть (под горизонтальной осью)
- Однако при таком искажении нижняя часть лабиринта становится менее стройной (все дорожки имеют переменную ширину)

- Более элегантное решение опирается на продолжение верхних концентрических полуокружностей вниз. Такую форму, в частности, мы видим на античных критских монетах (хотя чаще на них изображен квадратный лабиринт, подчиняющейся тем же правилам построения)
- К сожалению, при таком способе рисования приходится пожертвовать «крестом» и опирающимся на него простым алгоритмом, описанным выше