Оцени вероятность события в спектре вариантов

Удобный инструмент оценки целостности представлений учащихся об изучаемом явлении (2007)

•  От наиболее вероятного события – к полному спектру
•  Механизм подсчета баллов и «профиль уверенности»

От наиболее вероятного события – к полному спектру вариантов

Авторский коллектив, разрабатывающий проект по российской истории, предложил сценарий интерактивной игры, в которой от ученика требовалось оценить вероятность того или иного поворота в судьбе жителя Российской империи XIX века. На каждом шаге тренажера нужно было отвечать на вопрос типа: «Из предложенных вариантов развития событий выберите наиболее вероятный». Тренажер снабжался большим количеством информационных блоков, помогающих осознать реалии соответствующей эпохи и прийти к правильному выводу.

Однако сразу выявились методические недостатки рассматриваемой идеи. Во-первых, нередко выбор наиболее вероятного развития событий относительно прост, в то время как самые содержательные вопросы ставят перед учащимися именно отброшенные варианты. Во-вторых, информационная насыщенность тренажера оставалась практически неиспользованной сильными учениками, которые быстро находили правильные ответы и поэтому не читали пояснений. То есть тренажер хотя и содержал полезные для сильных учеников сведения, но никак не стимулировал их изучать. В-третьих, никак не оценивалось количественное значение вероятности события – насколько один из сценариев вероятнее другого.

Анализ предложенной модели позволил разработать методически более интересное решение, технически трудно осуществимое «на бумаге», но легко поддерживаемое при использовании компьютера. Суть нового тренажера состоит в следующем: существенно информативнее задавать вопрос не в форме выбора одного из вариантов, а в форме выбора распределения вероятностей по всему возможному спектру вариантов.

То есть от ученика требуется не просто указать, например, что вероятнее для дворянина – карьера военного или гражданская карьера – а численно оценить вероятность каждого из событий. Поскольку общая вероятность должна быть равна 100%, помимо предложенных для рассмотрения содержательных вариантов существует и выбор «Иное», также оцениваемый количественно.

Освещение темы в виде полного спектра вариантов позволяет гораздо глубже освоить учебный материал.

Эскизы технической реализации (наполнение и дизайн условные):

Увеличить изображение в отдельном окне   Постановка задачи.

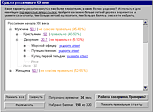
Увеличить изображение в отдельном окне   Полное дерево вариантов.

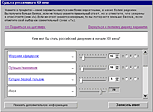
Увеличить изображение в отдельном окне   Выбор распределения вероятности на отдельном шаге.

Механизм подсчета баллов и «профиль уверенности»

Поскольку стандартный способ сверки ответа с эталонным в данной задаче неэффективен, для подсчета степени успешности ответа применяется гибкая шкала, обладающая следующими особенностями:

  • Правильный ответ – это ответ, попадающий в определенный диапазон (например, считать правильным ответ 50±5%).
  • Некоторая окрестность вокруг правильного ответа также оценивается – как ответ, близкий к правильному (например, за ответ «60%» к предыдущему примеру можно давать половину возможных баллов, а за «65%» не давать уже ничего).
  • Помимо правильности ответа учащегося, оценивается степень его уверенности в своем ответе.

На последнем пункте стоит остановиться подробнее. Автоматическое тестирование знаний обладает существенным недостатком в сравнении с очным опросом – преподаватель никак не может оценить уверенность учащегося в своем ответе. Таким образом, статистика стандартного компьютерного теста лишает преподавателя важной информации, которая могла бы способствовать лучшему пониманию проблем ученика.

Вот почему была введена простейшая шкала для оценивания степени уверенности отвечающего при выборе того или иного ответа. Каждый ответ сопровождается шкалой с радио-кнопками «не уверен» (?) – «нейтрально» (о) – «уверен» (!). Если ученик дает ответ и уверен, что ответ правильный, он отметит эту свою высокую степень уверенности и система начислит за правильный ответ больший балл. Но если ученик все же ошибся, то в той же ситуации он будет «оштрафован» системой сильнее. И наоборот – если ученик заведомо не уверен в своем ответе и честно в этом признается, то даже если ответ действительно окажется неправильным, штраф за ошибку будет меньше. Стремление набрать как можно больший балл будет стимулировать ученика отображать степень уверенности в каждом своем ответе.

Для преподавателя, разумеется, важнее не набранный учеником балл, а образующийся «профиль уверенности», который позволит гораздо лучше понимать взаимосвязь уровня реальных знаний учащегося с его самооценкой.

Формально подсчет баллов выглядит так:

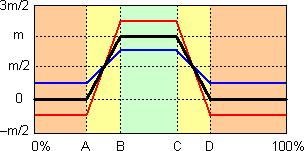
Для каждого варианта автором указываются 4 числа: A, B, C, D (по возрастанию, но могут и совпадать).

  • числа B и C определяют диапазон «правильно» (зеленая облась);
    за ответ, попадающий в этот диапазон, дается N = m баллов,
    где m – максимум, определяемый автором для каждого варианта отдельно;
  • числа A и D определяют диапазоны «почти правильно/не совсем правильно» (желтая область);
    за ответ, попадающий в этот диапазон, дается 0 < N < m баллов (линейная зависимость).

Кроме того, при присуждении баллов учитывается степень уверенности, высказанная отвечающим:

  • если уверенность нейтральная, то ничего не меняется и присуждается N' = N баллов (черный график)
  • если уверенность = !, то присуждается N' = N + k * (N – m/2) баллов (красный график – для k = 1/2)
  • если уверенность = ?, то присуждается N' = N – k * (N – m/2) баллов (синий график – для k = 1/2)
  К началу страницы