Типология моделей динамической математики

2. Манипулятивные модели для исследования

При создании статичных чертежей специфические возможности "Математического конструктора" используются лишь в небольшой степени. Мы уже отметили ключевую особенность построений в среде динамической геометрии: любые чертежи в "Математическом конструкторе", в отличие от начерченных на бумаге или на классной доске, относятся не к индивидуальной геометрической фигуре, а к целому непрерывному семейству фигур.

2.1. Совершаем открытие

Ученика вряд ли удивит, что при деформации треугольника луч, построенный как биссектриса его угла, всегда будет делить этот угол пополам – ведь мы именно так он и построен. Но если провести все три биссектрисы, то мы увидим, что они будут всегда пересекаться в одной точке, хотя эту точку мы и не строили – она возникла "сама". А это уже маленькое геометрическое открытие!

И такое открытие может перевернуть весь ход урока – от заунывного изложения "фактов", пусть даже сопровождаемого пассивным иллюстрированием, вы переходите к активному стимулированию творческого потенциала учеников, развиваете в них навык видеть, формулировать и понимать геометрические закономерности, существенно увеличиваете степень эмоциональной вовлеченности и запоминаемость изучаемого материала. Вот более сложная модель такого типа.

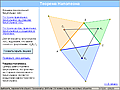Пример: Теорема Наполеона Иллюстрация Интерактивная модель-апплет

2.2. Ставим численный эксперимент

Все расстояния, углы и площади в "Математическом конструкторе" легко измеряемы. Это позволяет проводить численные экспериментальные наблюдения, которые могут вести к самостоятельному открытию тех или иных фактов.

Пример: Сумма расстояний до сторон равностороннего треугольника Иллюстрация Интерактивная модель-апплет

2.3. "Черный ящик"

Нравятся ученикам и задания типа "черный ящик", в которых, наблюдая за изменениями одних элементов чертежа при перемещении других элементов, учащиеся должны разгадать скрытый связывающий их "механизм". Например: дана фигура и ее образ при некотором движении. Требуется указать вид движения и его параметры.

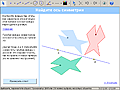Пример: Отгадай преобразование Иллюстрация Интерактивная модель-апплет

2.4. Выбери правильный ракурс

Специфическим классом задач, в которых манипулирование компьютерной моделью предоставляет ученику качественно новые возможности, являются стереометрические чертежи. Развитие пространственного воображения – одна из важнейших целей при изучении стереометрии. Нередко в стереометрической задаче достаточно взглянуть на пространственную конструкцию с нужной точки – и принцип решения станет понятен без долгих объяснений.

Пример: Сечение тетраэдра Иллюстрация Интерактивная модель-апплет

2.5. Определи граничные значения

Другой тип математического эксперимента, проводимого при помощи конструктора, – исследование пограничных и крайних ситуаций. Пусть, например, вы показали ученикам как строится треугольник по трем сторонам. А затем стали менять длину исходных отрезков – и вдруг треугольник "исчез". Так вы совершенно органично пришли к содержательной задаче о наличии и числе решений в зависимости от исходных данных. Рассмотрим более сложный пример такого рода, в котором поиск переходов геометрической конструкции "в новое качество" существенно облегчается с помощью компьютера.

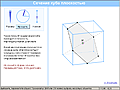Пример: Сечение куба плоскостью Иллюстрация Интерактивная модель-апплет

2.6. Исследуем геометрическое место точек

В последних версиях "Математического конструктора" появилась функция построения геометрического места точек. В предыдущих версиях она была представлена в "урезанном", хотя и вполне содержательном варианте – как рисование растрового следа движущейся точки. Эта функция открывает новую обширную область для экспериментов и исследования – разнообразные кривые. Преимущества, которые здесь обеспечивает компьютер, очевидны.

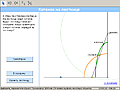Пример: Котенок на лестнице Иллюстрация Интерактивная модель-апплет

Мы смоделировали известную задачу о "котенке на лестнице". Модель позволяет не только увидеть траекторию точки на отрезке постоянной длины, скользящем своими концами по сторонам прямого угла (эллипс), но и проследить за ее эволюцией при изменении положения точки. Когда точка в середине отрезка эллипс превращается в окружность, что несложно доказать.

2.7. Исследуем графики функций

Очень полезной, особенно в связи с алгебраическими задачами с параметрами, является возможность построения графиков функций, зависящих от параметра, и исследовании их при изменении параметра. В качестве примера вернемся к уравнению, рассмотренному в п. 1.3, заменив в нем основания логарифма и степени произвольным числом.

Пример: Исследуйте зависимость числа корней уравнения от параметра Иллюстрация Интерактивная модель-апплет

Модель позволяет увидеть качественную картину зависимости числа корней от параметра и приближенно определить значения a, при которых оно изменяется. Точное решение – отдельная задача, в которой компьютер выступает лишь подспорьем (и это хорошо!).

Читать дальше >>